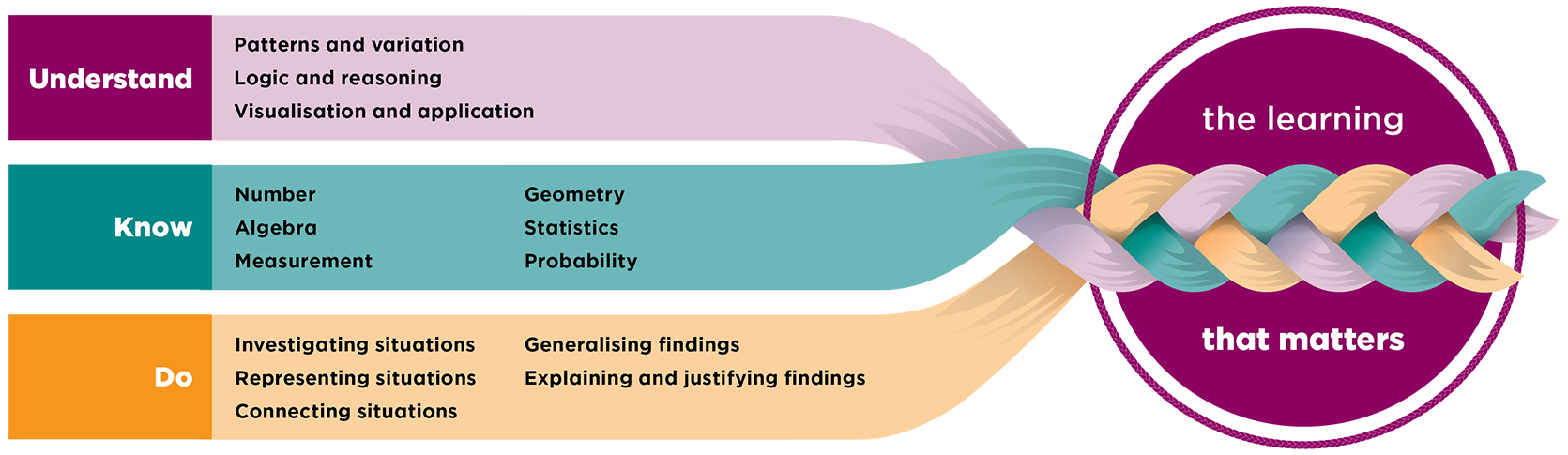
This page provides the progress outcome and teaching sequence for Phase 3 (years 7-8) of the Mathematics and statistics learning area of the New Zealand Curriculum, the official document that sets the direction for teaching, learning, and assessment in all English medium state and state-integrated schools in New Zealand. In mathematics and statistics, students explore relationships in quantities, space, and data and learn to express these relationships in ways that help them to make sense of the world around them. Other parts of the learning area are provided on companion pages.
We have also provided the Maths Years 0-8 curriculum in PDF format. There are different versions available for printing (spreads), viewing online (single page), and to view by phase. You can access these using the icons below. Use your mouse and hover over each icon to see the document description.
File Downloads
No files available for download.
Te Mātaiaho | The New Zealand Curriculum Mathematics and statistics: Phase 3 – Years 7‑8 |
Seeing ourselves in the wider world and advocating with and for others |
Progress outcome by the end of year 8
The critical focus of phase 3 is for all students to see themselves in the wider world and to advocate with and for others. Students use logic and reasoning to identify and solve problems, make connections between mathematical and statistical concepts, and investigate patterns and variation. They communicate mathematically and statistically, using notation, conventions, and vocabulary to clearly explain and justify their approaches to solving problems. Students select, use, and adapt representations to visualise and extend their reasoning (e.g., number lines to represent integers, equations to represent linear patterns). They make generalisations and identify unknown quantities (e.g., the size of angles) and use data visualisations to investigate claims and make conjectures.
The phase 3 progress outcome describes the understanding, knowledge, and processes that students have multiple opportunities to develop over the phase.
The phase 3 progress outcome is found in the table below.
Teaching sequence
Seeing ourselves in the wider world and advocating with and for others |
This section describes how the components of a comprehensive teaching and learning programme for the mathematics and statistics learning area are used during the third phase of learning at school.
Throughout phase 3, demonstrate, highlight, and affirm an attitude of exploration, enthusiasm, and curiosity towards mathematical and statistical endeavour and challenge, holding high expectations for every student. In this phase, students critically reflect on others’ reasoning, evaluating their logic and asking questions for clarification. To promote this, facilitate ongoing discussions and reflections about established expectations for interactions in mathematical and statistical learning, reinforcing that all students will be involved. Support increasing agency for students in making decisions about investigations and problem solving (e.g., while planning their approach, selecting representations, justifying their findings).
Continuously monitor students’ cognitive load, reasoning, questions, and use of representations, and respond quickly to address any issues and misconceptions. Ensure teaching builds on what students already understand, know, and can do.
Number
During year 7 | During year 8 | Teaching considerations | |
|---|---|---|---|
Number structure |
|
(e.g., 0.01 = 1—100 = 10-2) | Represent and order numbers using place-value (PV) expanders or charts and number lines. |
find the highest common factor (HCF) of two numbers under 100, and find the least common multiple (LCM) of two numbers under 10 |
| Represent factors using factor trees, or systematic lists. Connect HCFs to simplifying fractions, and LCMs to renaming fractions. Generalise conjectures about prime or composite numbers by investigating factors. | |
|
| Investigate and generalise divisibility tests for composite and prime numbers, and connect the results to square and cube numbers and square roots. Investigate and explain patterns in repeated multiplication and represent them using exponent notation. Connect prime and composite numbers with factors, and represent a number as a product of its prime factors (prime factorisation). | |
Operations |
|
| Explain efficient methods for supporting estimation (e.g., when adding a long list of numbers, look for numbers that can be grouped and summed to roughly 10, 100, 1000). Connect operations to benchmarks to make estimates (e.g., 73% is roughly 3—4) Explain and justify findings, by connecting to estimates and other checking methods such as using the inverse operation. |
|
| ||
|
| Investigate patterns in multiples in 100s boards and multiplication charts to generalise divisibility rules. | |
| Explain and demonstrate efficient methods using worked examples, including:
Investigate, explain, and justify which method (including the use of digital tools) best suits a given situation. Have students practise decoding and solving word problems and representing them as equations. Represent and make sense of remainders as fractions, as decimals, and when rounded to the nearest whole number. | ||
|
| ||
|
| Use worked examples to demonstrate a step-by-step layout with only one equal sign per line. Demonstrate how to use the mnemonic GEMA in relation to the order of operations: grouped, exponents, multiplicative (÷ and ×), additive (+ and –). | |
|
| Generalise that a positive number has an opposite negative number, and that when they are added, the answer is zero (e.g., 4 + –4 = 0). Explain how to:
Investigate adding and subtracting integers, using number lines and two-sided counters. Explain the direction of movement on a number line when adding and subtracting integers, and generalise that:
Investigate situations where negative integers are used (e.g., temperature, altitude, debt, profit and loss). | |
Rational numbers |
|
| Explain and represent:
Explain and demonstrate converting a fraction to a decimal or percentage by connecting to the understanding of fractions as quotients (e.g., 5—12 = 5 ÷12). Connect to known benchmarks for comparing and converting (e.g., 7—12 is a little more than 6—12 which is a half or 50%). |
|
| ||
|
| Represent decimals using PV expanders or charts, and generalise that multiplying by a power of 10 moves each digit that number of places to the left, and dividing by a power of 10 moves each digit that number of places to the right. | |
|
| Explain simplifying fractions and finding equivalent fractions by using HCFs and LCMs | |
|
| Explain the vertical column method for multiplying decimals, making an estimate before calculating. Connect to the multiplicative identity to generalise that multiplying a whole number by a decimal less than one results in a product less than the original whole number. | |
|
| Represent situations involving percentages using bar models to show parts of a whole. Explain how to find a percentage of a whole by using the decimal equivalent to multiply the whole (e.g., 35% of 120 = 0.35 × 120) or by finding 10%, 5%, or 1% of the whole and using operations (e.g., finding 35% of 120 by finding 10%, multiplying this by 3 to get 30%, then adding half of 10% – 12 × 3 + 6 = 42). | |
|
| Demonstrate and explain renaming fractions, using ideas about equivalence and by finding HCFs and LCMs. | |
|
| Connect methods for operating on whole numbers with operating on decimals, making an estimate before calculating. Investigate situations where decimals are compared and the differences between them found (e.g., sporting event times and distances). Have students practise decoding and solving word problems and representing them as equations. | |
|
| Investigate proportional reasoning in situations such as mixing paints, cooking from recipes, and sharing resources. Represent situations involving proportional reasoning using diagrams and comparison bar models. Connect proportional reasoning to multiplicative thinking and equivalent fractions. | |
Financial mathematics |
|
| Explain and justify ‘best deals’, considering personal priorities. Represent financial plans for practical situations using digital tools such as spreadsheets. Investigate situations where there are financial percentage losses or gains (e.g., calculating discounts or profits, statistics in the media about growth or decline). Connect the ideas of loss and debt with integers. Explain, using worked examples, finding a percentage discount by subtracting from the whole or by multiplying the whole by a decimal fraction (e.g., a 35% discount on $180 = $180 – (0.35 × $180), or 0.65 × $180). |
|
|
Algebra
During year 7 | During year 8 | Teaching considerations | |
|---|---|---|---|
Equations and relationships |
|
| Have students practise writing equations to represent word problems. Demonstrate solving one- or two-step equations and using the inverse operation to check findings. |
|
| Investigate variable values in practical situations with familiar formulae (e.g., for area, volume, speed). Have students practise substituting measurements or given values into formulae. | |
|
| Represent terms in algebraic expressions using algebra tiles. Represent algebraic expressions and equations using the conventions of algebra (e.g., 3 × b or b × 3 is written as 3b). At year 8, explain how to simplify algebraic expressions by collecting like terms together. At year 8, investigate systematic expansion approaches, including expansion tables, connecting to the distributive property. | |
|
| Represent a pattern using a table, model, or diagram, and use it to generalise a rule for the pattern. Use the rule and an XY graph to justify a conjecture for another term in the pattern. Investigate the history, meaning, and structure of growing patterns (e.g., tukutuku, other well-known patterns such as the Fibonacci sequence). | |
Algorithmic thinking |
|
| Connect an algorithm with an operation such as the vertical-column method for multiplication or with the procedure for adding fractions. Represent algorithms using flow charts, numbered step-by-step instructions, or digital tools. Explore algorithms by investigating:
|
Measurement
During year 7 | During year 8 | Teaching considerations | |
|---|---|---|---|
Measuring |
|
| Connect to benchmarks to make estimations. Have students practise the accurate use of rulers, scales, timers, protractors, thermometers, and measuring jugs in practical situations. Represent all written measurements with their units. Select appropriate tools and units for a situation, and explain and justify choices. |
|
| ||
|
| Connect measurement conversions with multiplying and dividing by powers of 10 (e.g., 2.05 L = 2050 mL). Investigate measurement conversion situations in which all four operations are applied to whole-number and decimal measures. | |
|
| Investigate the relationship between speed, distance, and time in practical situations, such as timing how long it takes to walk or run a certain distance. Have students practise substituting values into the speed formula. Connect finding the value of variables in the speed formula with solving algebraic equations and multiplication and division operations. | |
|
|
| |
Perimeter, area, and volume |
|
| Investigate perimeter, area, and volume, including finding missing lengths, in practical situations. Connect calculations with factors, multiples, and the commutative and associative properties. Represent working for calculations using a clear layout and by sketching composite shapes to show partitioning. Generalise the formulae for finding the area of triangles and volume of triangular prisms, and have students practise substituting measurement values into them. Connect the formulae with spatial representations. |
Geometry
During year 7 | During year 8 | Teaching considerations | |
|---|---|---|---|
Shapes |
|
| Use and create a range of 2D and 3D shapes, including shapes that draw on tactile materials, diagrams, and digital tools. Investigate ways of classifying shapes, including by creating algorithms and using Venn diagrams and tables. |
|
| Investigate using digital tools and protractors to explore angles. Investigate unknown angles to generalise the following rules:
Represent the value of an unknown angle using an equation and angle notation. | |
Spatial reasoning |
|
| Represent plan views and nets, using sketches on grid paper, digital tools, and physical models (e.g., blocks, cardboard nets). Connect to measurement procedures when creating sketches and models. |
|
| Explain and demonstrate resizing a shape using a centre of enlargement within the shape. Investigate transforming shapes to generalise which properties (angles, side lengths, area, orientation) do not change under transformation, and test the resulting generalisations using tracing paper, rulers, and protractors. Investigate the meaning of kōwhaiwhai patterns and other artefacts, and describe the use of transformations in them. | |
Pathways |
|
| Use maps of familiar and unfamiliar locations to:
Connect pathways to:
Investigate the navigating techniques of Māori and Pacific voyagers for locating position and finding the direction of travel. |
Statistics
During year 7 | During year 8 | Teaching considerations | |
|---|---|---|---|
Problem |
|
| Show, with student input, how to pose investigative questions, clearly identifying the variable, the group of interest, and the intent. Connect investigative questions with conjectures about expected findings. |
Plan |
| Explain and discuss ethical practices for the collection and use of data. Represent planning using a planning tool to outline methods of data collection, ‘who’ and what to measure, and how. Show, with student input, how to pose data-collection and survey questions. Explain the variables and group or groups of interest in secondary datasets. Investigate how survey and data collection questions can be misinterpreted, leading to unreliable data. | |
Data |
|
| Show, with student input:
Connect multiple variables for individuals, explaining that most datasets use a table design in which each row focuses on an individual and each column includes the data on multiple individuals for one variable. |
Analysis |
|
| Show, with student input, how to:
Explain how different data visualisations have different features and how to describe them in context (e.g., in relation to the middle, distributional shape, joint and conditional proportions, long-term trends) |
Conclusion |
|
| Show, with student input, how to:
|
Statistical literacy |
|
| Show, with student input, how to:
|
Probability
During year 7 | During year 8 | Teaching considerations | |
|---|---|---|---|
Probability investigations |
|
| Investigate, using the statistical enquiry cycle, games of chance, other everyday chance-based situations, patterns in possible outcomes, and theoretical and experimental distributions. Represent probability outcomes (theoretical and experimental) using lists, tables, tree diagrams, tally charts, visualisations of distributions, words, numbers, and technology. Explain how to describe and use probability concepts (e.g., outcomes, events, trials, models; theoretical and experimental probability; with and without replacement; the law of large numbers; probability estimates, probability distributions; chance, randomness, and variation). Connect anticipated outcomes with theoretical and experimental distributions. Connect probabilities with proportional reasoning, fractions, and percentages, and with relative frequencies from data investigations. |
Critical thinking in probability |
| Show, with student input, how to:
| |
The language of mathematics and statistics: Phase 3
Year 7 | Year 8 | |
|---|---|---|
Number |
|
|
Algebra |
|
|
Measurement |
|
|
Geometry |
|
|
Statistics |
|
|
Probability |
|
|
Abstract |
Symbolic representation of a concept. |
Acceleration |
Acceleration or accelerated learning is where students are enabled to learn concepts and procedures more rapidly than the expected rate of progress. Accelerated learning approaches involve teaching students year-level content and experiences and supporting them with appropriate scaffolds to make this work accessible. |
Additive identity |
Zero will not change the value when added to a number. For example, 16 + 0 = 16. |
Algorithm |
A set of step-by-step instructions to complete a task or solve a problem. |
Algorithmic thinking |
Defining a sequence of clear steps to solve a problem. |
Argument |
Providing an idea or finding that is based on reasoning and evidence. |
Associative property |
A property of operations when three numbers can be calculated (addition or multiplication) in any order without changing the result. For example, (4 + 3) + 7 = 4 + (3 + 7) because 7 + 7 = 4 + 10, and (4 x 3) x 5 = 4 x (3 x 5). |
Assumptions |
A proposition (a statement or assertion) which is taken as being true with respect to a given context. |
Attribute |
A characteristic or feature of an object or common feature of a group of objects —such as size, shape, colour, number of sides. |
Base 10 |
Our number value system with ten digit symbols (0-9); the place value of a digit in a number depends on its position; as we move to the left, each column is worth ten times more, with zero used as a placeholder; to the right, the system continues past the ones’ column, to create decimals (tenths, hundredths, thousandths); the decimal point marks the column immediately to the right as the tenths column. |
Benchmarks |
A reference point that we can use for comparison or estimation. For example, “My finger is about one centimetre wide.” |
Categorical variables |
A variable that classifies objects or individuals into groups or categories. For example, hair colour, breed of dog. |
Chance |
The likelihood that an outcome will occur. |
Claim |
A statement of what the student believes to be correct. |
Commutative property |
In addition and multiplication, each number can be operated in any order. For example, 5 + 6 = 6 + 5. |
Compose and decompose |
Compose is to make a shape using other shapes. Decompose is to break a shape into other shapes. |
Comparison investigative question |
An investigative question that compares a variable across two clearly identified populations or groups. For example, “I wonder if girls in our class tend to be taller than boys in our class?” |
Conceptual understanding |
The comprehension of mathematical and statistical concepts, operations, and relations by connecting related ideas, representing concepts in different ways, identifying commonalities and differences between aspects of content, communicating their mathematical and statistical thinking, and interpreting mathematical and statistical information. |
Conjecture |
A statement whose truth or otherwise is not yet determined but is open to further investigation. |
Constant |
A constant term is a fixed value that will not change. |
Continuous materials |
Models based on relative length or area, such as a number line, fraction wall, bar model. |
Data |
A collection of facts, numbers, or information; the individual values of which are often the results of an experiment or observations. |
Data ethics |
The principles behind how data is gathered, protected, and used; at the core of ethical practice is the need to do good and to do no harm. |
Data visualisations |
A graphical, tabular, or pictorial representation of information or data. |
Deduction |
Make a conclusion based on knowledge, definitions, and rules. |
Digital tools |
Digital applications, calculators. |
Discrete materials |
Separate objects that can be counted and grouped. For example, counters, ice block sticks. |
Discrete numerical variables |
Variables that can be counted and have a limited range of possibilities. For example, number of students in each team, the result of rolling a die. |
Disinformation |
False information spread deliberately to deceive others. |
Distribution |
In mathematics, distribution describes spreading terms out equally across an expression; in statistics, distribution describes how data values are spread across the range of values collected. |
Distributive property |
An operation is said to be distributive over another operation if it can take priority over the operation used for combination within brackets. For example, 6 × 17 = 6 × (10 + 7) = (6 × 10) + (6 × 7) = 60 + 42 = 102. |
Efficient |
A procedure is said to be efficient when it is carried out in the most simple and effective way. |
Element in a pattern |
In a repeating pattern, an element is the repeating core. |
Equation |
A number statement that contains an equal sign. The expressions on either side of the equal sign have the same value (are equal). |
Equivalent fraction |
Two different fractions that represent the same number are referred to as equivalent fractions. For example, 1—2, 2—4, 3—6, and 4—8 are equivalent fractions because they represent the same number. |
Estimate |
A rough judgement of quantity, value, or number. In statistics, an assessment of the value of an existing, but unknown, quantity. In probability, the probability of an outcome in an experiment. |
Event |
One or more outcomes from a probability activity, situation, or experiment. |
Evidence |
Information, findings, data that support (prove) a statement or argument. |
Expression |
Two or more numbers, operations or variables connected by operations. Expressions do not include an equal or inequality sign. |
Families of facts |
A group of equations that use the same numbers. For example, 3 x 2 = 6, 2 x 3 = 6, 6 ÷3 = 2, 6 ÷ 2 = 3. |
Generalisation |
To recognise and describe patterns in relationships. |
Growing pattern |
A pattern where there is a constant increase or decrease between each term. For example, 5, 10, 15, 20. |
Horizontal method |
Representing the operation as an equation across the page, often partitioning one of the numbers into tens and units. For example, 16 + 23 = 16 + 20 + 3. |
Inequality |
A statement in which one number or expression is greater or less than another. |
Inference |
Making a conclusion based on evidence and reasoning. |
Informal unit |
A non-standard unit used to measure. For example, blocks, pens, fingers. The informal units used should all be the same size. |
Interpret |
To make meaning from something. |
Inverse operations |
The opposite operation, so addition is inverse to subtraction, and multiplication is inverse to division. They are useful to check calculations. For example, to check 4 x 5 = 20, we can see if 20 ÷5 = 4. |
Limitations |
Possible missing evidence or information. |
Mathematical modelling |
An investigation of the relationships and behaviours of quantities in physical, economic, social, and everyday contexts; used to analyse applied situations and make informed decisions, starting the model with forming assumptions. |
Misconception |
A misunderstanding about a procedure, method or definition in mathematics or statistics. This could be about which procedure is needed, how the procedure or method should be followed or an incorrect definition. For example, thinking that 2.5 is the decimal form of 2/5. |
Misinformation |
Incorrect information (mistakes). |
Multiplicative identity |
When a number is multiplied by 1, it does not change its value. For example, 15 x 1 = 15. |
Number sentence |
An equation or inequality expressed using numbers and mathematical symbols. For example, 10 + 10 = 3 + 7 + 5 + 5. |
One step transformation |
One change in a shape's position or size. For example, a triangle is flipped (reflected). |
Ordinal |
The numerical position of the element in the sequence. For example, first, second, third. |
Orientation |
The angle that an object is positioned. |
Outcomes |
A possible result of a trial of a probability activity or a situation involving an element of chance; could also refer to a result or a finding. |
Partition and regroup |
Partitioning is the process of "breaking up" numbers. For example, 55 = 50 + 5. |
Primary data |
Data collected first-hand for a specific purpose. For example, a survey, experiment, or interview. |
Probabilistic thinking |
Considering the likelihood (chance) of an outcome occurring; this is based on logic and reasoning. |
Probability experiment |
A test that can be carried out multiple times in the same way (trials). The outcome of each trial is recorded. |
Procedural fluency |
Choosing procedures appropriately and carrying them out flexibly, accurately, and efficiently. It is not the same as memorisation of facts and steps; rather it is being able to activate what you know and when to use it. |
Procedure |
A sequence of operations carried out in a specific order, such as the procedure to multiply two numbers, or the procedure to measure an object. |
Quantifying |
Expressing a quantity using numbers. |
Rational number |
All integers, fractions, and decimals. |
Reasoning |
Analysing a situation and thinking and working mathematically to arrive at a finding. |
Relational |
Symbols that show relationships between elements (terms) in an expression. For example, =, <, > |
Repeating pattern |
A pattern containing a 'unit of repeat'. For example, red, green, blue, red, green, blue. |
Secondary data |
Data collected by someone else, or a process, and/or obtained from another source. For example, online, books, other researchers. |
Subitise |
Instantly recognise the number of items in an arrangement without counting. |
Summary investigative question |
A question that asks about the overall distribution of the data or what is typical and reflects the population or group. For example, “I wonder how many pets are in our class? I wonder what the heights of the students in the class are?” |
Tangible and intangible |
Tangible is an object that can be touched. For example, a group of blocks. Intangible is a quality or measurement that cannot be touched. For example, colour or length. |
Term in a pattern |
One of the numbers in a pattern or sequence. For example, for 2, 4, 6, 8, the second term is 4. |
Theoretical probability |
A calculation of how likely an event is to occur in a situation involving chance. |
Uncertainty |
In probability, when the chance of an event occurring is unknown. |
Unit of repeat |
The part of a repeating pattern that repeats. The part is made up of several elements |
Variables (statistics and algebra) |
A property that may have different values for different individuals (statistics) or that may have different values at different times (statistics and algebra). |
Variation |
The differences seen in the values of a property for different individuals or at different times. |
Vertical column method |
The method for solving an operation by recording numbers in columns according to place value, working down the page. |
Visualisation |
To mentally represent and manipulate. |